DEHB: EVOLUTIONARY HYPERBAND FOR SCALABLE, ROBUST AND EFFICIENT HYPERPARAMETER OPTIMIZATION
By Noor Awad,
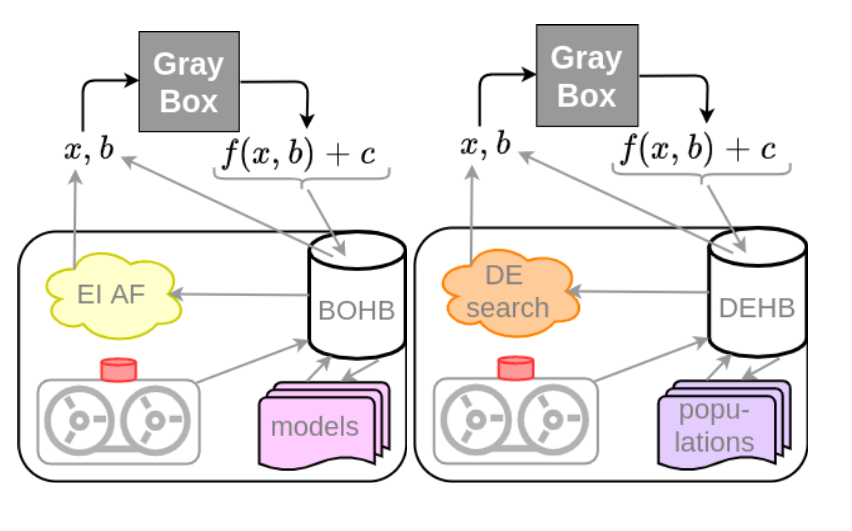
Modern machine learning algorithms crucially rely on several design decisions to achieve strong performance, making the problem of Hyperparameter Optimization (HPO) more important than ever. We believe that a practical, general HPO method must fulfill many desiderata, including: (1) strong anytime performance, (2) strong final performance with a large budget, (3) effective use of parallel resources, (4) scalability w.r.t. the dimensionality and (5) robustness & flexibility. These desiderata drove the development of BOHB [Falkneret al., 2018], which satisfied them by combining the best features of Bayesian optimization (BO) via Tree Parzen estimates (TPE) [Bergstra et al., 2011] (in particular, strong final performance), and the many advantages of bandit-based HPO via Hyperband. While BOHB is among the best general-purpose HPO methods we are aware of, it still has problems with optimizing discrete dimensions and does not scale as well to high dimensions as one would wish. Therefore, it does not work well on high-dimensional HPO problems with discrete dimensions and also has problems with tabular neural architecture search (NAS) benchmarks. This post presents DEHB which is the new successor of BOHB that replaces the BO component with the evolutionary search approach of Differential Evolution (DE) (as the figure below shows) to yield a new general optimizer to solve a broad range of HPO benchmarks and NAS problems.
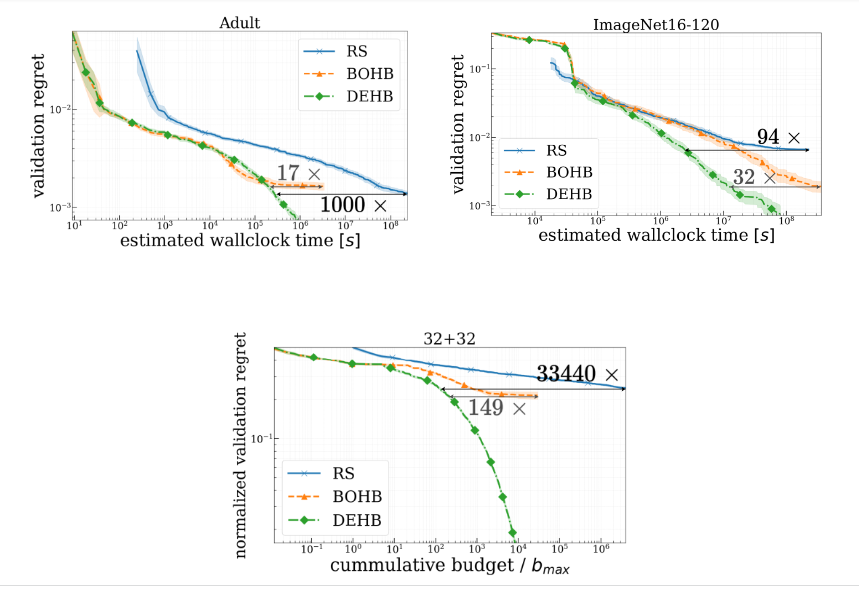
DEHB in particular is up to 1000 times faster than random search (RS) (Left plot) and up to 32 times faster than BOHB (right plot) on HPO problems; on toy functions, these speedup factors even reached 33 440 and 149, respectively (bottom plot).
Hyperband and Differential Evolution
HPO as a black-box optimization problem can be broadly tackled using two families of methods: model-free methods, such as evolutionary algorithms (i.e. Differential Evolution DE), and model-based methods (Bayesian Optimization). DE and BO are the two main components that form DEHB.
Hyperband
HB is a multi-armed bandit method which dynamically allocates different resources to a set of random configurations, and uses a simple heuristic, Successive Halving (SH) with simple random search repeatedly to allocate more resources (budget $latex r$) to promising configurations $latex n$. HB iterates the following steps:
- runs many configurations on a small budget
- increases the budget for the best ones
- terminates a constant fraction at each step to limit the computational cost
Differential Evolution
DE is a simple, well-performing EA to solve a variety of optimization problems, and starts by initializing a population space of N individuals uniformly at random in the search range. Then it iterates 3 basic steps:
- Mutation which is responsible to generate a new mutant vector based on weighted difference vector $latex v_{i,g}= x_{r_1,g} + F\cdot(x_{r_2,g} – x_{r_3,g})$ where $latex F$ is a scaling factor and is within (0,1]
- Crossover which uses a simple binomial operation to select values from $latex v_{i,g}$ with a probability $latex p$ (called crossover rate) and $latex x_{i,g}$ otherwise to generate the final offspring $latex u_{i,g}$
- Selection uses the better of $latex x_{i,g}$ and $latex u_{i,g}$ for the members of population for the next generation
DEHB: Evolutionary-based Hyperband
DEHB combines the best of both DE and HB, and maintains a \textit{subpopulation} for each of the fidelity levels such that no random sampling occurs and DE evolution runs instead with information flows from the subpopulations at lower budgets to those at higher budgets through a modified DE mutation. DEHB runs several iterations. The first iteration in DEHB is similar to vanilla HB, and random search is used to initialize the first subpopulation at lowest fidelity. Every subsequent SH bracket begins by reusing the subpopulation updated in the previous SH bracket and carrying out a DE evolution, and the information flows from the subpopulations at lower budgets to those at higher budgets through the modified DE mutation. Unlike in vanilla DE, in DEHB, the mutants involved in DE evolution are extracted from the parent pool instead of the population itself. This allows the evolution to incorporate and combine information from the current budget, and also from the lower budgets.

The runtime of DEHB does not grow over time in stark contrast to BO methods whose time complexity is in cubic in the number of functions evaluations. SH brackets can be asynchronously distributed over free workers with the use of a central DEHB Orchestrator that keeps a single copy of all DE subpopulations allowing for asynchronous and immediate DE.
Applications/Experiments
DEHB has been evaluated on a broad collection of HPO and NAS benchmarks, and compare DEHB to a broader range of baseline algorithms and compute the average relative rank over time for each algorithm.
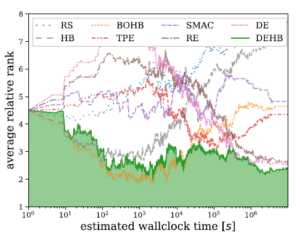
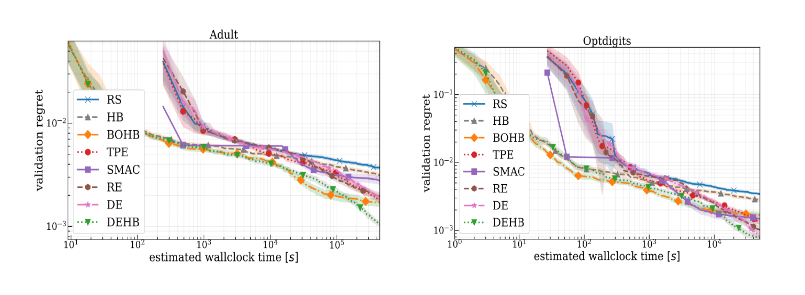
Optimization of Surrogates for Feedforward Neural Networks
We optimize six architectural and training hyperparameters of a feed-forward neural network on six different datasets from OpenML. Adult and Optdigits are examples where DEHB is achieving the best final score.
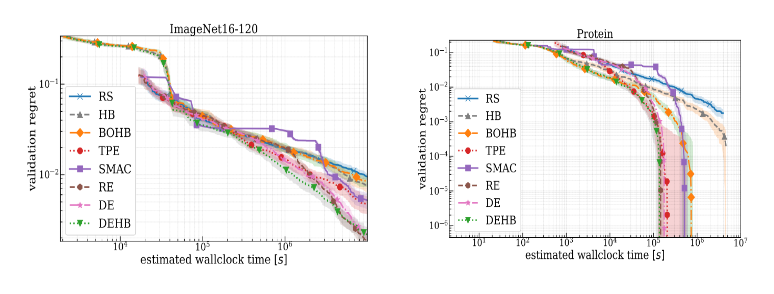
Optimization of Neural Architecture Search
A broad range of NAS benchmarks is used, and here we show the performance of ImageNet16-120 from NAS-201 and the Protein Structure dataset provided in NAS-HPO-Bench.
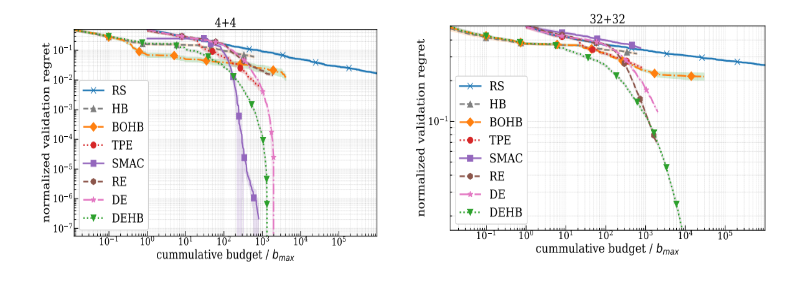
Optimization of Artificial Toy Function: Stochastic Counting Ones
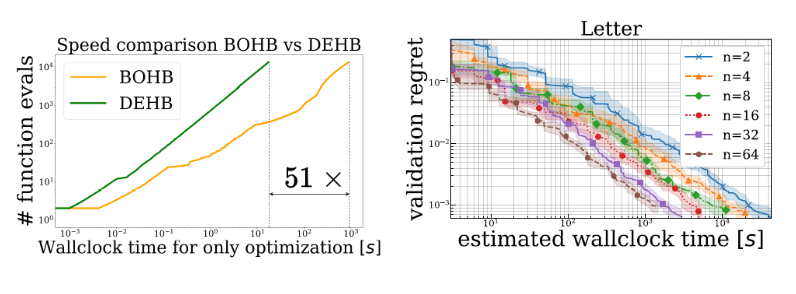
This toy benchmark is useful to assess scaling behavior and ability to handle binary dimensions. Here we present the 8 and 64-dimensional spaces in which DEHB shows superior performance.
What else?
You can find more details and further experiments in our paper. Please also try DEHB to optimize your HPO settings (https: //github.com/automl/DEHB). Finally, we’re happy to receive feedback.