Authors: Mohammad Loni, Aditya Mohan, Mehdi Asadi, and Marius Lindauer
TL, DR: Optimizing activation functions and hyperparameters of sparse neural networks help us squeeze more performance out of them; thus helping with deploying models in resource-constrained scenarios. We propose a 2-stage optimization pipeline to achieve this.
Motivation: Sparse Neural Networks (SNNs) – the greener and learner cousin of deep neural networks – are very good candidates for deploying models in resource-constrained applications that can also be safety critical. In such scenarios, every single percent of performance gain matters. However, SNNs suffer from a decrease in accuracy, particularly at high pruning ratios, making practical deployment difficult [1,2]. In this work, we explore ways of mitigating this accuracy drop by understanding the role of activation functions and hyperparameters in mitigating this accuracy drop in SNNs and using these insights to develop a method aimed at juicing as much performance as we can out of SNNs during inference.
Core Insights:
- Activation Functions Influence SNN Accuracy: Conventionally, the ReLU activation function is the go-to choice, but our research suggests that this might not always be the best fit for SNNs. This seemingly insignificant selection can partially explain the dip in accuracy when models go sparse. Thus, by thinking outside the box and trying alternative activation functions, we can crank up performance.
- Fine-tuning Hyperparameters for SNNs: Traditionally, we’ve been fine-tuning sparse networks with the same hyperparameters used for their dense counterparts. However, this one-size-fits-all approach overlooks the unique characteristics of sparse models, leading to an avoidable hit in accuracy. By giving SNNs their own optimized hyperparameters, we can drive their performance up.
Method: To tackle this issue head-on, we introduce a novel approach called Sparse Activation Function Search (SAFS) that focuses on learning activation functions for sparse networks and a separate hyperparameter optimization regime.
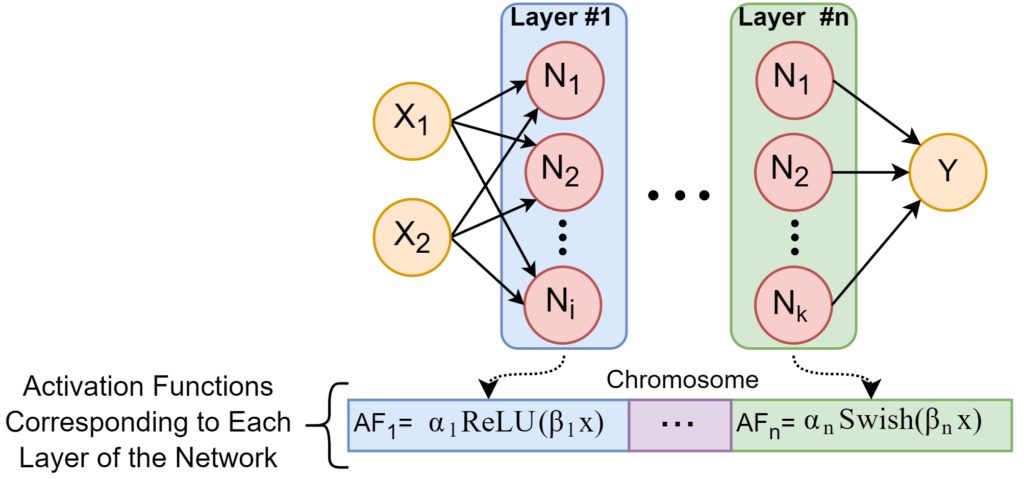
To learn activation functions, we model an activation function as shown below

Thus, learning an activation function entails learning the unary operator and the scaling parameters $\alpha, \beta$. We break this down into two steps:
- We learn the unary operator by selecting it from a set of already available popular activation functions. This selection is done per layer. Thus, for a 16-layer NN, we would be selecting potentially 16 different activation functions. We use Late Acceptance Hill climbing [5] for this step.
- We then interleave the search for scaling parameters with the fine-tuning step and thus, achieve this at no additional cost
We finally wrap an HPO regime around this pipeline, thus, allowing us to achieve performance gains from the combination of activation function selection and HPO.
Experimental Results: We conducted experiments on popular deep neural network models, including LeNet-5, VGG-16, ResNet-18, and EfficientNet-B0, trained on MNIST, CIFAR-10, and ImageNet-16 datasets. The results demonstrated that SAFS achieved significant improvements in accuracy compared to conventional approaches (Table 1).

Potential Future Work: We believe this opens up new avenues of research into methods that can improve the accuracy of SNNs. We hope that our work motivates engineers to use SNNs more than before in real-world products as SAFS provides SNNs with similar performance to dense counterparts. Some immediate directions for extending our work are (i) leveraging the idea of accuracy predictors [3] in order to expedite the search procedure. (ii) SNNs have recently shown promise in application to techniques for sequential decision-making problems such as Reinforcement Learning [4]. We believe incorporating SAFS into such scenarios can help with the deployment of such pipelines.
If you are interested in the project, please check out our paper and our GitHub page.
References
[1] Sehwag, V., Wang, S., Mittal, P., and Jana, S. (2020). Hydra: Pruning adversarially robust neural networks. In Larochelle et al. (2020).[2] Mousavi, H., Loni, M., Alibeigi, M., and Daneshtalab, M. (2022). Pr-darts: Pruning-based differentiable architecture search. CoRR.
[3] Li, G., Yang, Y., Bhardwaj, K., and Marculescu, R. (2023). Zico: Zero-shot nas via inverse coefficient of variation on gradients. CoRR.
[4] Vischer, M., Lange, R., and Sprekeler, H. (2022). On lottery tickets and minimal task representations in deep reinforcement learning. In Proceedings of the International Conference on Learning Representations (ICLR’22). Published online: iclr.cc.
[5] Burke, Edmund K., and Yuri Bykov. “The late acceptance hill-climbing heuristic.” University of Stirling, Tech. Rep (2012).